This week I can't resist the urge to say at least a few words about how we solve systems of ordinary differential equations. It's too important a topic to just hand-wave away.
Solving differential equations is an enterprise that goes back to Newton, who invented the field. The basic problem is simple: you have a differential equation that relates a function to its derivatives, and you know the value of the function and its derivatives at a point in time or space. You might even have a whole set of coupled differential equations, where coupled means that they share some values. This often happens in flow-related problems, for example: the out-flow term in one equation is equal and opposite to the in-flow term in the equation for the next bit of the system along, thanks to the magic of conservation laws, which enforce these equalities.
That's what we have with SEIRS equations for pandemics:
dE/dt = S*n*p*(I/N) - E'[Te] (1)
dI/dt = E'[Te] - E'[Ti] (2)
dR/dt = E'[Ti] - E'[Tr] (3)
dS/dt = E'[Tr] - S*n*p*(I/N) (4)where E, I, R and S are the number of people in the Exposed, Infectious, Recovered, and Susceptible states, Te, Ti, and Tr are the number of days from Exposure to Infectious, from Exposure to the end of the Infectious phase, and from Exposure to Susceptible again. N is the total number of people (thirty-eight million in the case of Canada), and n*p*(I/N) is the individual probability of getting infected each day, which when multiplied by S (the number of susceptible people) gives us the number of newly infected people. n is the number of people someone encounters each day, p is the probability that an encounter with an infected person will result in infection, and I/N is the probability that anyone a person meets is infectious.
I managed to completely mess up the expression S*n*p*(I/N) in my previous discussion, although in the code I've written it's correct. I only realize the problem because of the discipline that mathematical description imposes on me. People sometimes get uptight about how pedantic we have to be with mathematical descriptions or they become incoherent, but the reality is we have to be pedantic with any description of the world or it will become incoherent. It's just that without the formal guard-rails that mathematics gives us, we're rarely aware of that, at least not until the gulags and political re-education camps start overflowing. Sometimes not even then.
This set of pandemic equations, called a "SEIRS model", for "Susceptible, Exposed, Infectious, Recovered, Susceptible" after the stages people pass through, is clearly coupled: the various E' terms are shared between stages, as the number of people who leave one stage must be equal to the number entering the next.
E'[T] is the number of people who were newly exposed T days ago, and that is what drives all the dynamics. We can write the whole system in terms of the number of newly infected people T days ago: conservation laws ensure the states of the present are coupled by the facts of the past.
But how do we get from there to here? Knowing the past and how it was changing, how to we get to the present?
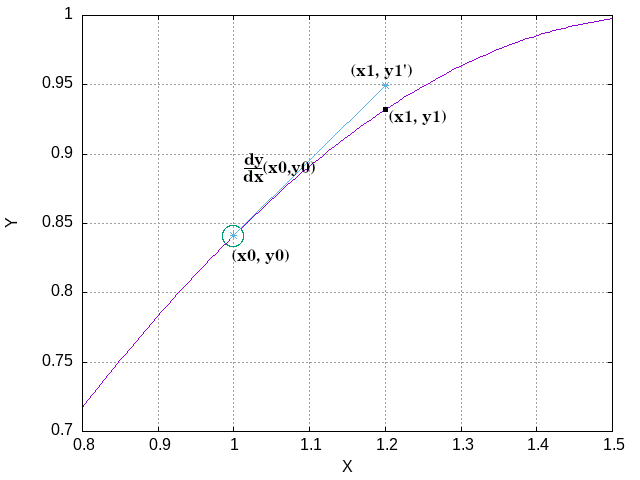
The basic idea hasn't changed since Newton's time: we know at some starting point x0 the value of the function we're interested in, which we'll call y0 = y(x0). We also know the slope at that point: if we don't, we can't solve the problem. These initial or boundary conditions are part of the problem statement, or we don't have a solvable problem.
Knowing the value y0 and the slope, we can estimate the value of y at some nearby point: y1 = y(x1) = y0+(x1-x0)*dy/dx
The trick here is that the slope isn't changing very quickly with x, so we can approximate the change over the whole interval from x0 to x1 with a single slope.
If the world is kind to us, this approach, known the Euler Method after German mathematician Leonard Euler, works somewhat poorly. If the world is unkind--the common case--it works very poorly, and if the world is really unkind the cumulative error is independent of the step size. This is the case for a circular orbit, for example: no matter how finely you divide it up, the error-per-step gets small in precise proportion to the number of steps.
If this seems all terribly boring, it's worth recalling that very nearly everything you can see right now that was made by human beings depends on the accurate solution of systems of differential equations for its existence. The computer you're reading this on, the furniture you're sitting on, the walls, the windows... all of that would not exist if we couldn't solve systems of differential equations, and you'd be sitting in a farmhouse reading a newspaper wondering if the spring planting was going to be any good.
It's not too much to say that the difference between the world of a century ago and the world of today is maybe one third due to our ability to solve differential equations better than previous generations, because that ability lets us design stuff with very little prototyping, and to solve problems that are simply inaccessible when working with physical prototypes, which can never be fully instrumented. Expert insight can do a lot, but expert insight informed by dynamical models is precisely the "standing on the shoulders of giants" that Newton attributed his success to.
The numerical systems we use to solve dynamical models can be instrumented in ways that allow us to "look inside" with a kind of numerical x-ray vision. For everything from electronics to mechanical and fluid-mechanical systems this ability to see inside our designs and get an idea of the value of stress or strain or whatever in places we could never actually get a stress or strain or whatever gauge in a physical prototype is a huge advantage.
But how do we do better than Euler's method?
There are a bunch of ways, but they all come down to the same basic idea: Euler's method gives us a more-or-less lousy approximation to (x1, y1), and we have an equation that lets us figure out dy/dx for any (x, y), so we can use our lousy approximation of (x1, y1) to get a lousy approximation of the slope at x1: dy/dx(x1,y1).
We can then take the average slope over the interval using the known value at the start and the poorly known value at the end. We can then repeat Euler's method with this average value of the slope to get a better approximation to (x1, y1).
And so on: this process can be iterated.
There are various technical tricks to make the iteration more numerically efficient, but the principle remains the same. For all well-behaved and most ill-behaved dynamical models this process converges quite quickly, and the standard workhorse for numerical solution goes by the name of the "fourth order Runge-Kutta method", after the two mathematicians who completed our iterative generalization of Euler's original approach a century or so ago. This method uses values at the middle of the interval as well.
The methods I've described here are part of a family called explicit finite difference methods. They are "explicit" in the sense that we can write down an equation for the next point in terms of the previous point and nothing else. Implicit methods solve for all the points at once, and can often be much more numerically efficient. This efficiency comes at the cost of complexity, and I'm a relentlessly simple-minded person, so while I use them when necessary I cherish the clarity of explicit methods.
As well as finite difference methods, which replace derivatives with slopes, there are finite element methods, which use a knowledge of what the solutions to a particular problem should look like to construct a linear combination of them that minimizes the residual error. These are used very heavily in mechanical engineering, and have a much shorter history than finite differences methods, which predate automatic computing machinery by more than a century.
In the modern world, electronic computers have made a huge amount of past work redundant. We can be relatively relaxed about the efficiency of our methods because we literally have billions of times more computing power available to us than the smartest people in the world had access to in 1950.
Even so, some problems remain a challenge.
Fortunately, pandemic modelling is not one of them, and I'll talk about what insights solving the SEIRS model equations can give us next week.
In the meantime: look around you. Your car, you lamp, your TV... all of them exist in the form they do, are as efficient and capable as they are, because engineers today know how to solve systems of differential equations better than we used to.
People should have at least some familiarity with the things that keep us alive: everything from farming to mining to mathematics. We're a species that gets a lot of mileage out of specialization, and the scope of the modern world makes it impossible to have more than a minimal awareness of a vast range of topics. But differential equations are important enough that they're worth spending a least a little of our precious attention on. And as we'll see next week, solving them can give us real insight into the world around us.